4603. Ê-edges
graph
You are given an acyclic directed graph, consisting of n
nodes and k edges. Find the number of edges in its transitive closure.
Transitive closure of graph G is a graph G', consisting of
all nodes of original graph G and such edges (u, v) that there is
a path from node u to v in graph G.
Knuth knows how to solve the problem. And what about you?
Input. The first line contains two numbers n and k (1 ≤ n, k ≤ 50000). Then k lines follow, each containing two
integers ai and bi, describing directed edge
from ai to bi (1 ≤ ai, bi ≤ n).
Graph doesn't contain loops, cycles and multiple edges.
Output. Print the number of edges in transitive closure.
Sample
Input
5 6
1 2
2 3
3 5
4 5
1 5
1 3
Sample
Output
7
SOLUTION
graphs – masks
Algorithm
analysis
The mask of subset
of vertices we shall call a sequence of 0 and 1 of length |V|. The masks will
be stored in an integer array (or
bit-set structure). Run the Depth-First Search on the given directed graph. For
each vertex v we will create a subset
of vertices reachable from v (not including v). If m1, …, mk are the masks of
children vertices v1, …, vk (in the Depth-First
Search tree) for the vertex v, then the mask of vertex v has the form:
m1 or … or mk
or 2v1 or … or
2vk
The number of edges
in the transitive closure outgoing from the vertex v, equals to the number of ones in the bit mask corresponding to v.
Example
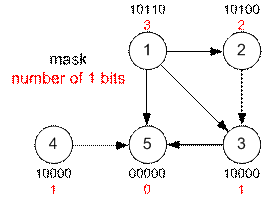
The lowest bit in
the mask corresponds to the vertex number 1. The total number of bits in all
masks is 3 + 2 + 1 + 1 + 0 = 7, that equals to the number of edges in the
transitive closure.
Algorithm
realization
The graph adjacency matrix we store in
array g. In DFS we
shall used an array used for already
traversed vertices. Array mask[i] stores a bit
mask for vertices, into which
there exist a path from i. bits[i] contains the number of bits in binary
representation of number i.
#define MAX 50100
vector <vector<int> > g;
int used[MAX], mask[MAX][MAX/32], bits[1<<16];
The depth first search from the vertex v.
void dfs(int v)
{
int i, j, to;
used[v] = 1;
for(i = 0; i < g[v].size(); i++)
{
to = g[v][i];
if(!used[to]) dfs(to);
For each son to of
vertex v do the operation mask[v] = mask[v] OR mask[to].
for(j = 0; j < MaskLen; j++) mask[v][j]
|= mask[to][j];
Add into the mask of vertex v the vertex to.
mask[v][to >> 5]|= 1 << (to & 31);
}
}
Preprocessing of array bits. The cell bits[i] contains the number of ones in binary
representation of a number i.
int gen(int mask)
{
int i;
if (!mask) return
0;
if (bits[mask]) return
bits[mask];
for(i = 0; i < 32; i++)
if (mask & (1 << i))
bits[mask] = gen(mask ^ (1 << i)) + 1;
return bits[mask];
}
The main part of the program. Read the input data.
memset(bits,0,sizeof(bits));
gen((1 << 16) - 1);
scanf("%d
%d",&n,&k);
g.resize(n);
while(k--)
{
scanf("%d %d",&i,&j);
g[i-1].push_back(j-1);
}
The cell of int
type 32 bits, and the graph contains n
vertexes. To store the mask of length n
bits it is sufficient to use an integer array of length MaskLen = ![]() .
.
MaskLen = (n + 31) / 32;
Run the Depth-First
Search, where the reachability masks for each vertex are created.
for(i = 0; i < n; i++)
if(!used[i]) dfs(i);
It remains to
calculate the number of ones in all masks mask[i] (0 ≤ i ≤ n – 1).
for(res = 0, i = 0; i < n; i++)
for(j = 0; j < MaskLen ; j++)
res += bits[mask[i][j] & 65535] + bits[(mask[i][j] >> 16)
& 65535];
Print the number of edges in transitive closure of the graph.
printf("%d\n",
res);
Realization
with bitset
#pragma comment (linker, "/STACK:100000000")
#include <cstdio>
#include <vector>
#include <bitset>
#define MAX 50100
using namespace std;
vector <vector<int> > g;
int used[MAX];
int res, n, k, MaskLen;
bitset<MAX> mask[MAX];
void dfs(int v)
{
int i, j, to;
used[v] = 1;
for(i = 0; i < g[v].size(); i++)
{
to = g[v][i];
if(!used[to]) dfs(to);
mask[v] |= mask[to];
mask[v].set(to);
}
}
int main(void)
{
int i, j, r;
scanf("%d %d",&n,&k);
g.resize(n+1);
while(k--)
{
scanf("%d %d",&i,&j);
g[i].push_back(j);
}
for(res = 0, i = 1; i <= n; i++)
{
if(!used[i]) dfs(i);
res += mask[i].count();
}
printf("%d\n", res);
return 0;
}